Lecture 07 着色-1 基本着色模型、光照和反射

1289字约4分钟

2024-12-19

1 着色

在计算机图形学中，着色指的是在物体上应用材质的过程.

如下图所示，一个光源照亮了几个茶杯，可以看到茶杯的颜色主要分为颜色变化剧烈的高光部分、颜色变化平缓的漫反射部分、没有直接光照但是被环境光线照亮的间接光照部分.

通常研究某一点（Shading Point）的着色，而非整个物体的着色.

在此之前我们需要规定观测方向 $\boldsymbol{v}$ 、光线方向 $\boldsymbol{l}$ 、物体的法线方向 $\boldsymbol{n}$ 和物体的表面参数（如颜色等）.

由于着色的局部性，我们对几个物体进行着色后，可以看到其明暗变化，而不能看到阴影. 因为着色过程不考虑光线的遮挡.

不同于镜面反射，漫反射的光射会向各个方向.

那么对于一个漫反射的物体，它在相机中的亮度应该如何计算呢？

我们使用光的能量来替代亮度.

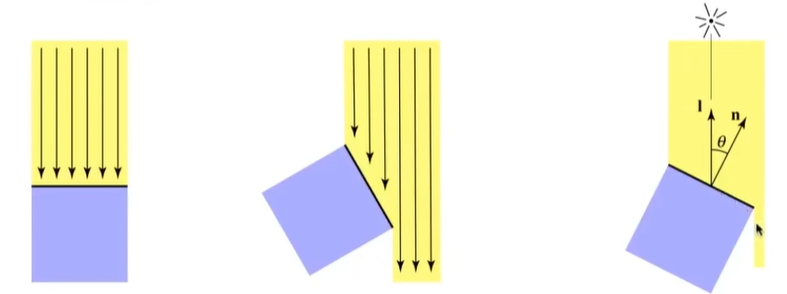
我们知道，当物体表面垂直于光线方向（或者说法线方向平行于光线方向）时，接收到光照的有效面积最大，接收到的能量也最多，在相机中表现的就越亮；而当物体表面平行于光线方向（也就是法线方向垂直于光线方向）时，物体接收到光照的有效面积为0，接收到的能量也为0，在相机中表现为黑色.

由下图我们可以理解，单位面积 $A_{unit}$ 内接收到光照的有效面积 $A$ 为

A = A_{unit} \cos\theta = \boldsymbol{l} \cdot \boldsymbol{n}

我们再考虑光源散发出的能量. 假设光源均匀散发能量，根据能量守恒定律，距离光源越远，单位面积内接收到的能量就越少.

假设距离光源单位距离的单位面积内接收到的能量为 $I$ ，那么简单计算就可以知道，距离光源 $r$ 的单位面积内接收到的能量为 $I/r^2$ .

综合上述内容，得到漫反射物体上一点处反射出的能量为：

L_d = k_d \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{l} \} }

式中， $k_d$ 是漫反射物体的反射率，一般和颜色等有关. 例如一个物体的反射率为1，就说明这个物体不吸收能量，将全部接收到的能量反射出去；而反射率为0的物体吸收全部的能量而不反射任何能量. 下图展示了 $k_d$ 对漫反射的影响.

由于漫反射的向各个方向反射的特性，相机在等距离的任何一个方向上观察物体，得到的结果应该是一样的. 也就是说，漫反射物体在相机中的亮度与观测方向无关.

在漫反射中，我们注意到高光部分的存在. 从实际出发我们知道，当我们的观察方向和反射方向接近的时候，我们就能看到高光.

在Blinn-Phong模型中，使用法线方向 $\boldsymbol{n}$ 和半程向量 $\boldsymbol{h}$ 来替代观察方向和反射方向. 其中半程向量的方向是入射方向和观察方向的角平分线.

不难得出

\boldsymbol{h} = \frac{\boldsymbol{v}+\boldsymbol{l}}{||\boldsymbol{v}+\boldsymbol{l}||}

于是在Blinn-Phong模型中，有

\begin{align*} L_s &= k_s \frac{I}{r^2} \max{\{0,\cos\alpha\}} ^p \\ &= k_s \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{h}\}} ^p \end{align*}

下图说明了 $p$ 的作用. 当 $p=1$ 时，我们发现，即使半程向量距离法线已经很远了，但是仍然具有可观的值，这就导致和实际情况不符合（通常我们见到到高光都是在一个很小的范围内）. 因此我们加入一个指数 $p$ 来缩小高光的可见范围.

下图中，每一排的 $k_s$ 保持不变，从左到右 $p$ 逐渐增大；每一列的 $p$ 保持不变，从上到下$k_s#逐渐增大.

我们假设物体任何一个点接收到的环境光照强度都是相同的.

L_a = k_a I_a

式中的 $I_a$ 是环境光照强度，可以近似认为一个常数， $k_a$ 是物体的反射率.

通过上述对漫反射、高光和环境光照的探索，我们知道，在Blinn-Phong反射模型中，物体的着色分为三部分进行.

\begin{align*} L &= L_a + L_d + L_s \\ &= k_a I_a + k_d \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{l} \} } + k_s \frac{I}{r^2} \max{\{0,\boldsymbol{n} \cdot \boldsymbol{h}\}} ^p \end{align*}