1 抗锯齿

在Lecture 05最后生成的“三角形”中，可以看到有很多的锯齿。为了避免这种情况，需要进行抗锯齿的操作.

1.1 采样

在拍照过程中，照片上的每个像素都是真实空间中一点的“样本”；在播放动画时，通过逐帧播放图像便形成了肉眼可见的连续的动画，这也可以认为是一种采样.

但是很明显，在采样过程中会有信息丢失等一系列问题，如下图的明显的摩尔纹. 这在图形学中称为Simple Artifact.

本质来说，产生Simple Artifact的原因是因为高频信号和低频采样不匹配.

一种抗锯齿的方式是，在采样之前先加一层模糊.

1.2 频域

1.2.1 傅立叶展开

任何一个函数都可以写成一系列正余弦函数和常数项的线性组合.

例如，下面这个函数可以近似表示一个方波：

$$f(x) = \frac{A}{2} - \frac{2A\cos(3t\omega)}{3\pi} + \frac{2A\cos(5t\omega)}{5\pi} - \frac{2A\cos(7t\omega)}{7\pi} + \dots$$

经过傅立叶级数展开，任何任何一个函数都可以分解成不同频率的波（也就是多项式中的各三角函数项）的线性组合.

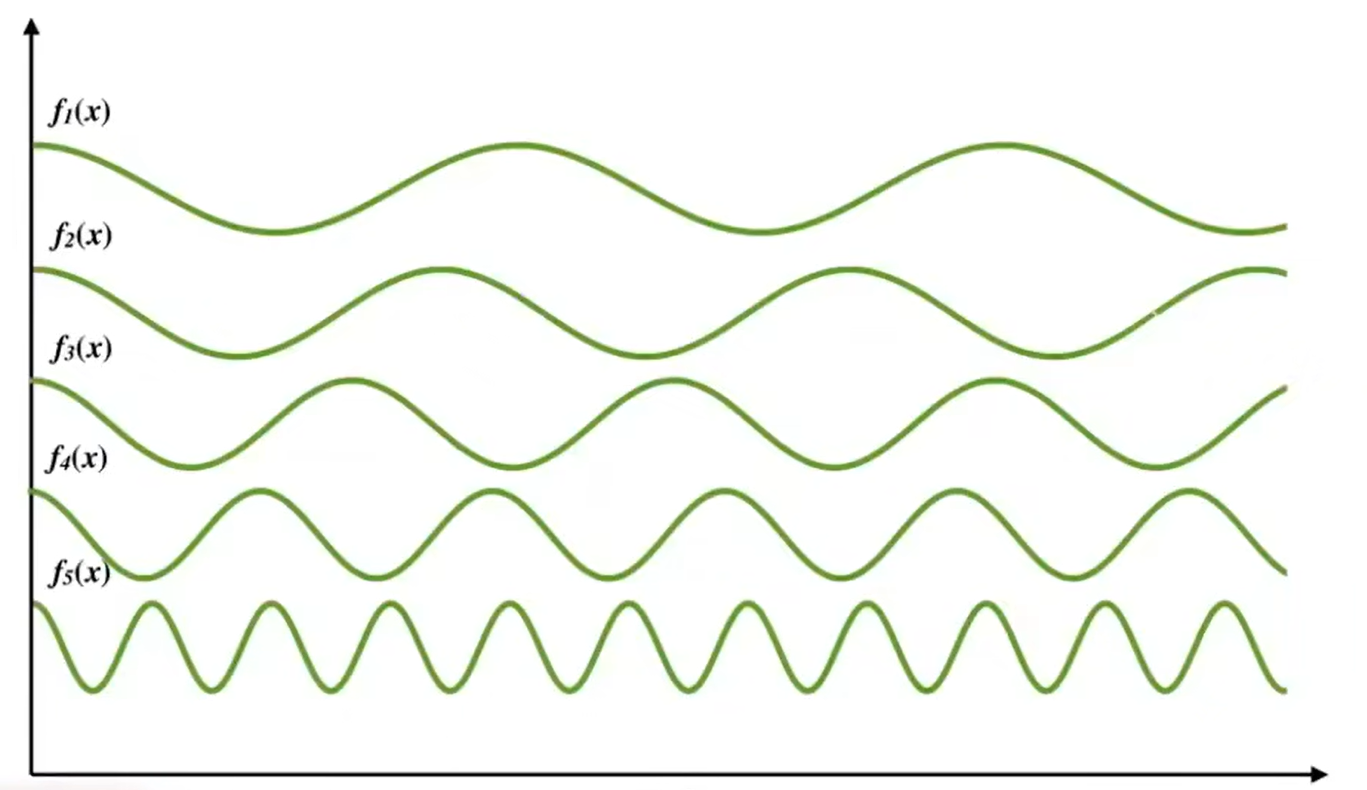
而当我们对这个函数进行低频采样时就会发现，在较低频率的波上，采样值的变化和真实值比较相似，而高频信息几乎完全丢失.

1.2.2 走样

在采样过程中会出现下面这种情况，即在某个频率采样下，两条频率完全不同的波采样得到的结果是相同的。这种情况就被称之为走样.

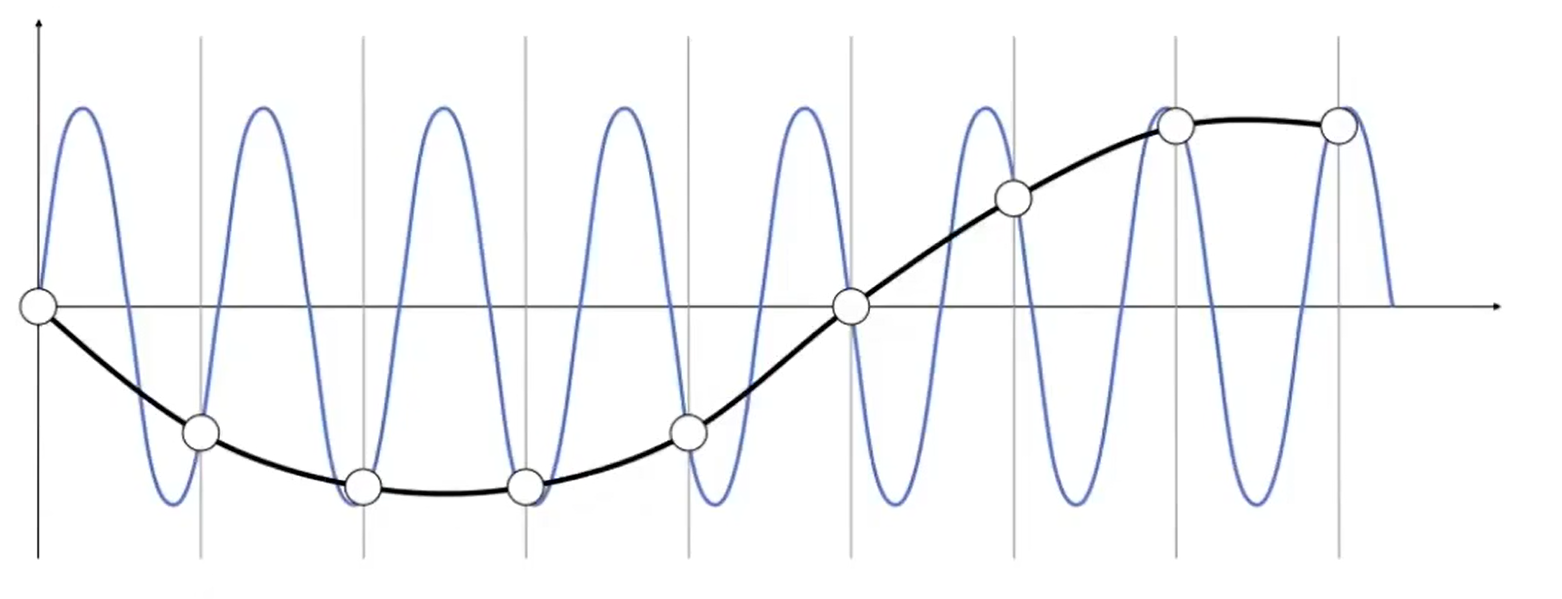
1.2.3 滤波

应用傅立叶变换，可以将时域转换为频域. 如下图所示，左侧是原图，右侧是它的频域图. 频域图的中心代表低频波段，周围代表高频波段，亮度代表该频率下的信息量. 观察频域图发现，在这幅图中低频信息较多，而高频信息较少，呈现出中心亮而周围暗的状态。

而我们人为去除掉某些波段就称为滤波. 保留高频、去除低频称为高通滤波，保留低频、去除高频称为低通滤波.

下图原图应用高通滤波后的结果. 可以看到，原图中的低频部分被去除，留下了变化剧烈的“边界”，也就是高频部分。

下图是原图应用低通滤波后的结果，图片整体变得模糊.

还有一些其他的滤波，可以从图像中提取出不明显的信息.

1.2.4 卷积

卷积可以看作一种“平均”，下图所示的卷积窗口可以在信号上滑动，取对应的三个窗口分别相乘再相加，得到中间对应的值.

则第三格的值应该为$3\times(1/4) + 5\times(1/2) + 3\times(1/4) = 4$

顺序滑动即可得到所有的值.

下图展示了卷积和频域的关系.

其中，

$$\frac{1}{9} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix}$$

被称为卷积核，它的卷积中心的值等于它周围八个像素和它自身的平均值.

这个滤波器是一个低通滤波器.

1.3 反走样

根据上面的分析，我们可以得到一种可行的反走样方案，即在采样之前先加一层模糊。更专业地说：在采样之前进行低通滤波.

经过低通滤波器

$$\frac{1}{9} \begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix}$$

滤波之后，原本三角形像素内部的值就从原来的0和1变成了一个浮点数：

直观地说，三角形覆盖的像素的面积比例转化为了像素的值.

但是计算这个面积比例又成为了新的难题.

1.3.1 超采样MSAA

由于精确求解三角形覆盖的像素面积比例需要消耗过多的计算资源，因此提出了一种近似方法.

这种方法将一个完整的像素划分为若干个子像素，判断每个子像素的中心是否在三角形内. 统计在三角形内的子像素的比例，即可得到近似值.

1.3.2 其他抗锯齿方案

• FXAA

  是一种后期图像处理方案. 将一副有锯齿的图像进行边界匹配等操作，更换为没有锯齿的边界.

• TAA

  在相邻两帧图像中，某些像素的位置应该也是相邻的，复用这些像素以达到抗锯齿的效果.

2 深度测试

深度测试用来解决不同远近、相互遮挡的三角形应如何在屏幕上显示的问题.

类比地说，在作油画时，画家们通常先画远处的物体，然后再一层一层画近处的物体. 这被称为画家算法.

但是对于下面这种情况，画家算法显然不太适用：

为了解决这个问题，引入Z-Buffer的概念. 在生成图像时，同步生成两张图像，一张用于记录颜色的Frame Buffer和一张用于记录深度的Depth Buffer.

Depth Buffer的基本思想是，初始化一个元素都为无穷大的Z-Buffer，然后遍历所有三角形中的所有像素，如果对应位置的像素的深度小于Z-Buffer中的值，就更新记录，否则不做操作. 如下图所示.