1 屏幕和像素

1.1 屏幕

对于图形学来说，屏幕可以抽象为一个像素的二维数组.

屏幕是一个典型的光栅化方法.

1.2 像素

像素是一个单色的正方形，像素的颜色可以由红色、绿色、蓝色三种颜色来表示.

本课程使用的屏幕坐标系是以右下角为原点，向右为$x$轴正方向的右手系，宽高分别为$w$个像素和$h$个像素. 像素的坐标用左下角的点的坐标来代替，像素坐标的取值范围为$(0,0)$到$(w - 1, h - 1)$之间的整数格点，像素$(x,y)$中心坐标为$(x+0.5, y+0.5)$.

如下图中蓝色像素的坐标可以被表示为$(2,1)$，其中心为$(2.5,1.5$).

2 光栅化

光栅化可以理解为把物体显示在屏幕上的过程.

2.1 视口变换

在Lecture 04 2.2中将模型透视投影为了标准立方体，接下来就要解决将模型显示在屏幕上的问题.

首先我们对模型的标准立方体进行正交投影，即令$z$坐标为$0$，此时其投影位于平面$[-1,1]^2$内.

然后把$[-1,1]^2$平面映射到屏幕$[0,w] \times [0,h]$中：

$$M_{viewport} = \begin{pmatrix} \frac{w}{2} & 0 & 0 & \frac{w}{2} \\ 0 & \frac{h}{2} & 0 & \frac{h}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

这个变换称为视口变换.

2.2 三角形的光栅化

得益于三角形的诸多良好性质，图形学中通常用三角形表示各种曲面. 因此各种模型的光栅化均可以转化为三角形的光栅化.

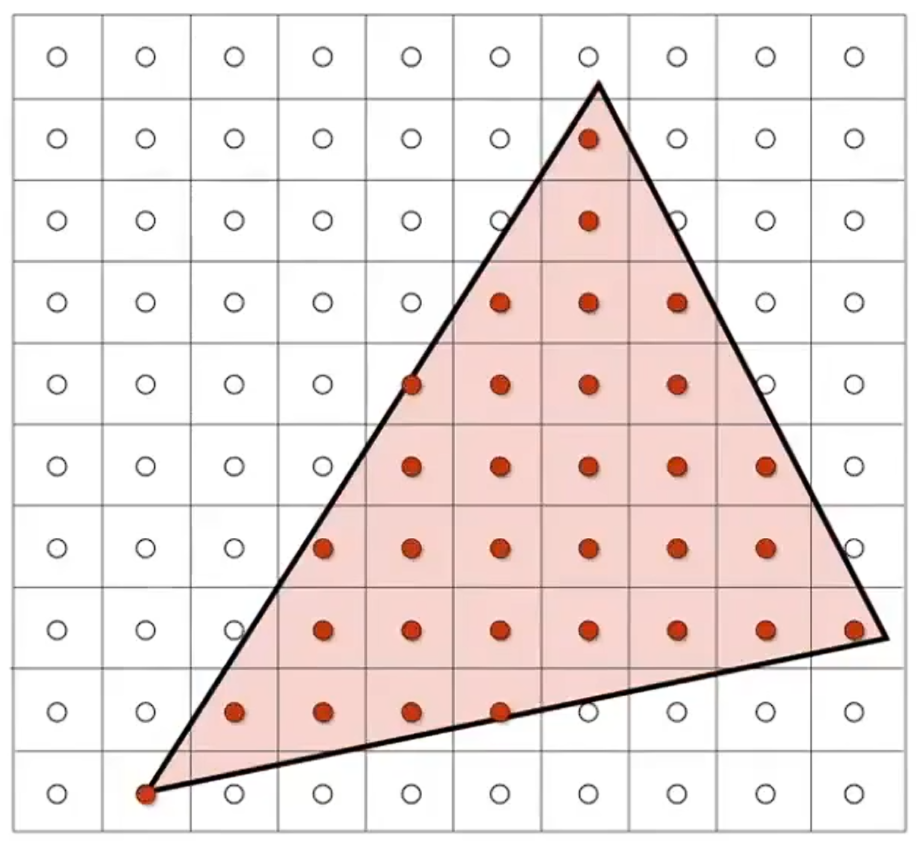
以下图为例将三角形覆盖到屏幕上，直观上可以认为：落在三角形内部的像素将其涂色，而三角形外部的像素不作处理. 那么三角形边缘处的像素应该如何判断？

只需要判断像素的中心是否在三角形内即可：

for(int x = 0; x < xmax; ++x)
{
  for(int y = 0; y < ymax; ++y)
  {
    image[x][y] = inside(tri, x + 0.5， y + 0.5)
  }
}

为了避免遍历所有屏幕像素，提出包围盒的概念：只判断包围盒内部的像素，而包围盒外部的像素直接判断为在三角形外.