一些约定……

课程默认使用列向量.

课程默认使用右手系（即使OpenGL中使用左手系）.

1 向量

向量是具有方向和长度的量，通常记为 $\vec{a}$ 或者粗体的$\boldsymbol{a}$.

本系列笔记采用打印体中较为美观的粗体写法.

对于由起点$A$和终点$B$定义的向量，则可表示为$\vec{AB}=B-A$.

在平面直角坐标系中，由原点指向$(x,y)$方向上的向量$\boldsymbol{a}$的可以被表示为$\boldsymbol{a}=(x,y)$.

1.1 向量的模

向量的长度被称为向量的模，记为 $||\boldsymbol{a}||$.

在平面直角坐标系中，若$\boldsymbol{a}=(x,y)^T$，则$|| \boldsymbol{a} ||= \sqrt{x^2+y^2}$.

根据向量的模可定义该方向上的单位向量，单位向量是长度为1的向量。与向量$\boldsymbol{a}$同方向的单位向量可以记为$\hat{a}={\boldsymbol{a}}/{||\boldsymbol{a}||}$.

1.2 向量的和

两个向量的和仍然是一个向量，并且满足平行四边形法则（三角形法则）.

在平面直角坐标系中，若向量$\boldsymbol{a} = (x_a,y_a)^T,\boldsymbol{b}=(x_b,y_b)^T$，则$\boldsymbol{a}+\boldsymbol{b}=(x_a+x_b,y_a+y_b)^T$.

1.3 向量的数量积（点乘）

向量的数量积是一个数，它没有方向.

$$\boldsymbol{a} \cdot \boldsymbol{b} = | \boldsymbol{a} || \boldsymbol{b} | \cos \theta$$

式中：$\theta$为两向量之间的夹角.

• 点乘可用来求夹角：

$$\cos \theta = \frac{\boldsymbol{a} \cdot \boldsymbol{b}}{| \boldsymbol{a} || \boldsymbol{b} |}$$

• 对于单位向量，有：

$$\cos \theta = \hat{\boldsymbol{a}} \cdot \hat{\boldsymbol{b}}$$

向量的数量积满足以下性质：

$$\boldsymbol{a} \cdot \boldsymbol{b} = \boldsymbol{b} \cdot \boldsymbol{a}$$

$$\boldsymbol{a} \cdot ( \boldsymbol{b} + \boldsymbol{c}) = (\boldsymbol{a} + \boldsymbol{b} ) \cdot \boldsymbol{c}$$

$$(k \boldsymbol{a}) \cdot \boldsymbol{b} = \boldsymbol{a} \cdot (k \boldsymbol{b}) = k(\boldsymbol{a} \cdot \boldsymbol{b})$$

在直角坐标系下，有：

$$\boldsymbol{a} \cdot \boldsymbol{b} = (x_a,y_a)^T \cdot (x_b,y_b)^T=(x_a x_b + y_a y_b)^T$$

$$\boldsymbol{a} \cdot \boldsymbol{b} = (x_a,y_a,z_a)^T \cdot (x_b,y_b,z_b)^T =(x_a x_b + y_a y_b +z_a z_b )^T$$

1.4 向量投影

一般称$\boldsymbol{b_\perp}$为向量$\boldsymbol{b}$在向量$\boldsymbol{a}$上的投影：

$$\boldsymbol{b_\perp}= k \hat{\boldsymbol{a}}$$

式中$k=||\boldsymbol{b}|| \cos\theta$.

• 可用于将一个向量分解为两个相互垂直的向量.

• 判断两个向量的大致方向.

1.5 向量的向量积（叉乘）

两个向量$\boldsymbol{a}$和$\boldsymbol{b}$的向量积是一个新的向量$\boldsymbol{c}$，它垂直于向量$\boldsymbol{a}$和向量$\boldsymbol{b}$张成的平面，方向满足右手定则，其模为$||\boldsymbol{a} \times \boldsymbol{b}|| = ||\boldsymbol{a}|| ||\boldsymbol{b}|| \sin\phi$.

• 向量积满足分配率.

$$\boldsymbol{a} \times (\boldsymbol{b} + \boldsymbol{c}) = \boldsymbol{a} \times \boldsymbol{b} + \boldsymbol{a} \times \boldsymbol{c}$$

• 向量积并不满足交换律. 交换后的向量积方向相反，而模相等.

$$\boldsymbol{a} \times \boldsymbol{b} = - \boldsymbol{b} \times \boldsymbol{a}$$

• 此外，一个向量和其本身的向量积为零向量.

$$\boldsymbol{a} \times \boldsymbol{a} = \boldsymbol{0}$$

• 向量数乘的向量积：

$$\boldsymbol{a} \times (k \boldsymbol{b}) = k(\boldsymbol{a} \times \boldsymbol{b})$$

在平面直角坐标系中：

$$\begin{align*} \boldsymbol{a} \times \boldsymbol{b} &= \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a &0 \end{pmatrix} \begin{pmatrix} x_b \\ y_b \\ z_b \end{pmatrix} \\ &= (y_a z_b - y_b z_a, z_a x_b - x_a z_b, x_a y_b - y_a x_b)^T \\ \end{align*}$$

如果令$x,y,z$三个坐标轴正方向上的单位向量为$\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$，则向量积可被表示为：

$$\boldsymbol{a} \times \boldsymbol{b} = \begin{vmatrix} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ x_a & y_a & z_a \\ x_b & y_b & z_b \end{vmatrix}$$

在计算机图形学中，向量积可用来判断“左和右”. 假设下图中的向量$\boldsymbol{a}$和$\boldsymbol{b}$在 $xOy$平面上，则根据右手定则，$\boldsymbol{a} \times \boldsymbol{b}$ 指向$z$轴正方向，那么我们认为$\boldsymbol{b}$在$\boldsymbol{a}$的左侧；同理，$\boldsymbol{b} \times \boldsymbol{a}$指向$z$轴负方向，那么我们认为$\boldsymbol{a}$在$\boldsymbol{b}$的右侧.

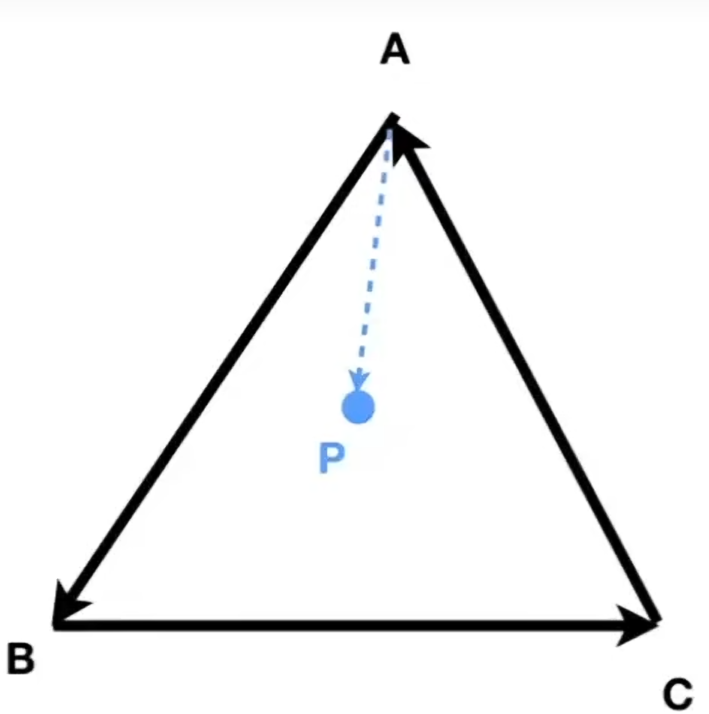
由上述规则可以进一步判断“内与外”. 依次做$\vec{AP}\times\vec{AB}, \vec{BP}\times\vec{BC}, \vec{CP}\times\vec{CA}$，若以上向量积指向的方向相同，则$P$点在三角形$ABC$的内侧，否则在外侧.

2 矩阵

2.1 矩阵的乘法

两个矩阵相乘，要求左边矩阵的列数和右边矩阵的行数相同，否则不能相乘.

$$A_{m \times n} B_{n \times t} = C_{m \times t}$$

矩阵$C$中的第$(i,j)$个元素为矩阵$A$的第$i$行向量和矩阵$B$的第$j$列向量的数量积. 即若设矩阵$A_{m \times n} = (a_1, a_2, a_3, \dots, a_n)^T, B_{n \times t}= (b_1, b_2, b_3, \dots, b_t)$，则：

$$\begin{align*} C_{m \times t} &= A_{m \times n} B_{n \times t} \\ &= \begin{pmatrix} \boldsymbol{a_1} \\ \boldsymbol{a_2} \\ \boldsymbol{a_3} \\ \vdots \\ \boldsymbol{a_m} \end{pmatrix} \begin{pmatrix} \boldsymbol{b_1} & \boldsymbol{b_2} & \boldsymbol{b_3} & \dots & \boldsymbol{b_t} \end{pmatrix} \\ &= (c_{ij}) \\ &= (\boldsymbol{a_i} \cdot \boldsymbol{b_j}) \end{align*}$$

• 矩阵的乘法不满足交换律.
• 但是矩阵的乘法满足结合律和分配率.

$$(AB)C=A(BC)$$

$$A(B+C) = AB + AC$$

$$(A+B)C=AC+AB$$

2.2 矩阵的转置

若矩阵$A=(a_{ij})$，将其行列对调，形成的新矩阵称为转置矩阵，记为$A^T$.

$$A^T = (a_{ji})$$

• 矩阵的转置满足“穿脱法则”：

$$(AB)^T = B^T A^T$$

2.3 单位矩阵和矩阵的逆

主对角线上的元素全为1，其余元素全为0的矩阵称之为单位矩阵.

$$I_n = \begin{pmatrix} 1,0,0,\dots,0 \\ 0,1,0,\dots,0 \\ 0,0,1,\dots,0 \\ \vdots,\vdots,\vdots,\ddots,\vdots\\ 0,0,0,\dots,1 \end{pmatrix}_n$$

如果一个矩阵和矩阵$A$相乘得到了单位矩阵，则称这个矩阵为矩阵$A$的逆矩阵，简称为矩阵$A$的逆，记为$A^{-1}$.

$$A A^{-1} = A^{-1} A = I$$

• 矩阵的逆满足“穿脱法则”：

$$(AB)^{-1} = B^{-1} A^{-1}$$